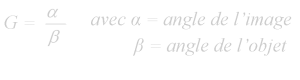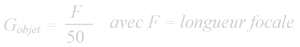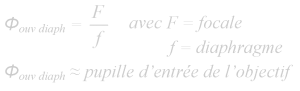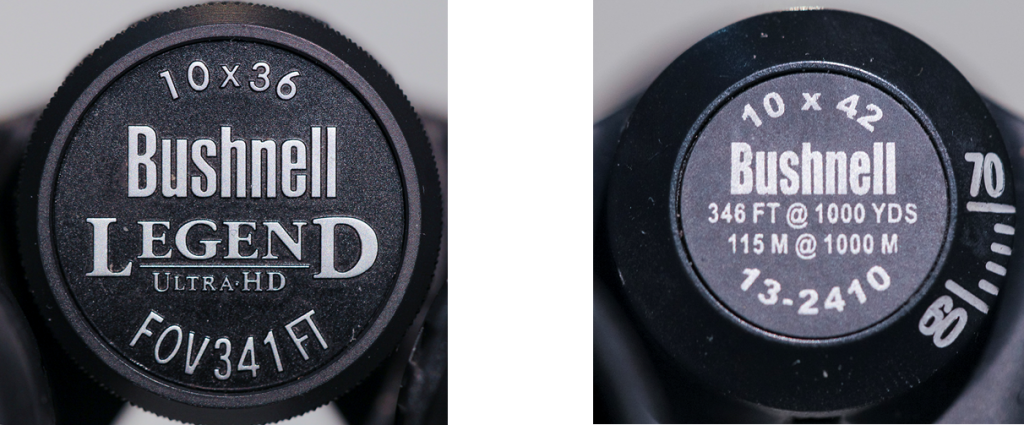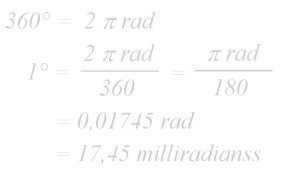Focale équivalente ou corrigée
- 17 juin 2020
Réflexion sur cette notion quelque fois mal comprise qu’est la focale équivalente ou corrigée 35 mm ou 24×36
En photographie, la distance focale équivalente en 35 mm (voir encadré) ou 24×36 est une mesure qui indique l’angle de vue particulier à un objectif d’appareil photo combiné à un type de pellicule ou de capteur de taille déterminée. Le terme provient de l’époque où la grande majorité des photos étaient faites avec des films 35 mm
Maintenant que les appareils photo numériques ont presque totalement remplacé les appareils photo argentiques, il n’y a plus de relation unique entre la distance focale d’un objectif et l’angle de vue, puisque celui-ci est aussi fonction de la taille du capteur, qui n’est pas standardisée comme l’était la taille du film. La distance focale équivalente en 35 mm d’un couple objectif-capteur donné est la distance focale qui serait nécessaire sur un appareil photo argentique 35 mm pour obtenir le même angle de vue.
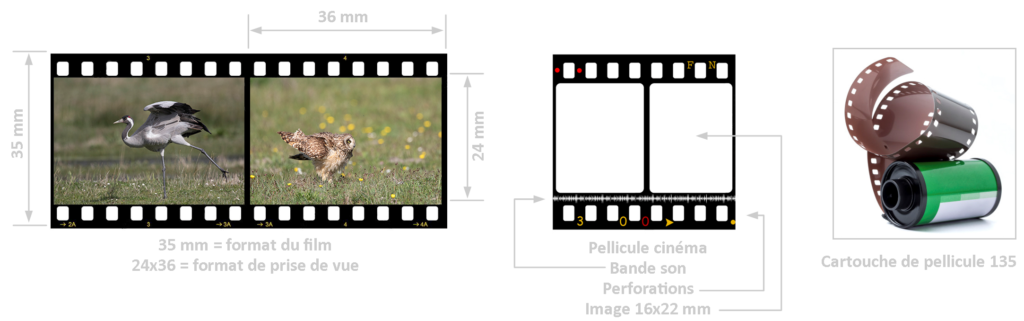
l faut différencier le « format de film » du « format de prise de vue ». Par exemple, un film 135 peut servir aussi bien à prendre des images classiques de 24 × 36 mm, 18x 24 mm (encore appelé demi-format) comme des images panoramiques de 24 × 65 mm. Lancé par Oskar Barnack (l’inventeur du Leica) en 1924, il s’agit à l’origine d’un film pour le cinéma. Les deux bandes de pellicule de chaque côté de l’image servent à perforer des trous d’entrainement et contient une bande magnétique pour le son. En photographie, elles serviront uniquement à perforer les trous qui entraineront la pellicule sur les tambours de l’appareil photographique. Le format 35 mm donnera la cartouche 135, un conditionnement commercialisé par Kodak à partir de 1934 permettant le chargement et la manipulation du rouleau en plein jour.
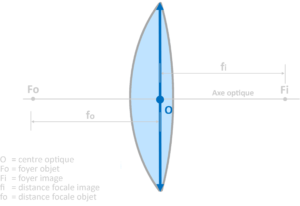 L’axe optique est une ligne imaginaire qui traverse la lentille en y pénétrant perpendiculairement au centre de sa face d’entrée. On pourrait le matérialiser en joignant les centres des deux sphères constitutives de la lentille. Schématiquement, le centre optique est le point situé à l’intersection de l’axe optique et du symbole de la lentille. Sa détermination exacte est complexe; disons simplement que tout rayon lumineux traversant la lentille via le centre optique n’est pas dévié, ne subit aucune réfraction.
L’axe optique est une ligne imaginaire qui traverse la lentille en y pénétrant perpendiculairement au centre de sa face d’entrée. On pourrait le matérialiser en joignant les centres des deux sphères constitutives de la lentille. Schématiquement, le centre optique est le point situé à l’intersection de l’axe optique et du symbole de la lentille. Sa détermination exacte est complexe; disons simplement que tout rayon lumineux traversant la lentille via le centre optique n’est pas dévié, ne subit aucune réfraction.
Le foyer image ou point focal image est l’endroit où se forme l’image d’un objet situé à l’infini. C’est donc le point de l’axe optique où convergent tous les rayons lumineux parallèles à celui-ci que l’on considère comme provenant de l’infini. Tous les rayons sont déviés excepté celui qui est confondu avec l’axe optique. La distance focale ou communément appelée focale est la distance qui sépare le centre optique de la lentille de son foyer image. En optique, le cheminement des rayons lumineux est parfaitement symétrique. De cette façon il existe aussi un foyer objet et une focale objet symétriques par rapport au centre optique de la lentille. Tout rayon lumineux issu du foyer objet de la lentille sont déviés et en ressortent parallèlement à l’axe optique de celle-ci.
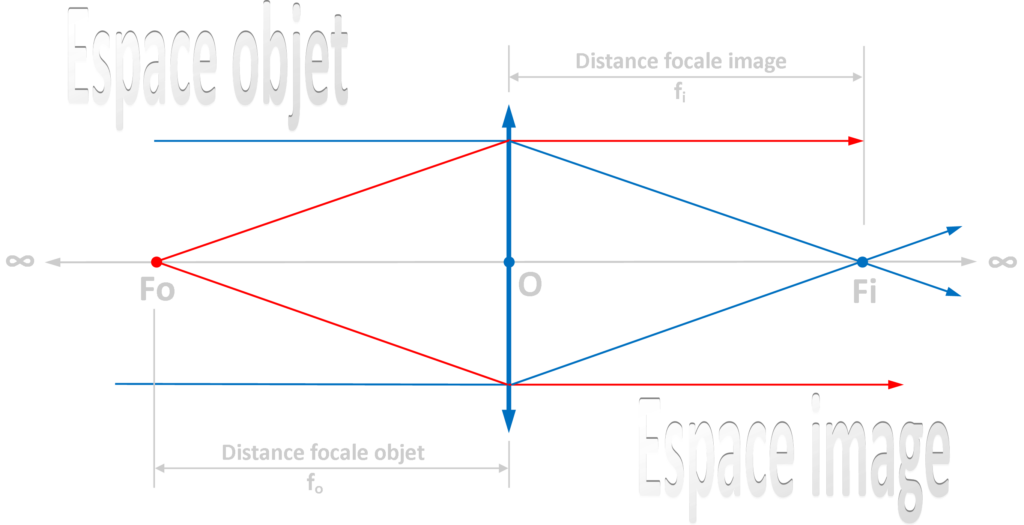
De ce qui précède, on peut déduire trois rayons lumineux importants. Ceux-ci ont un comportement invariable quelle que soit la position ou la forme de l’objet dont ils proviennent. On les appellera rayons particuliers.
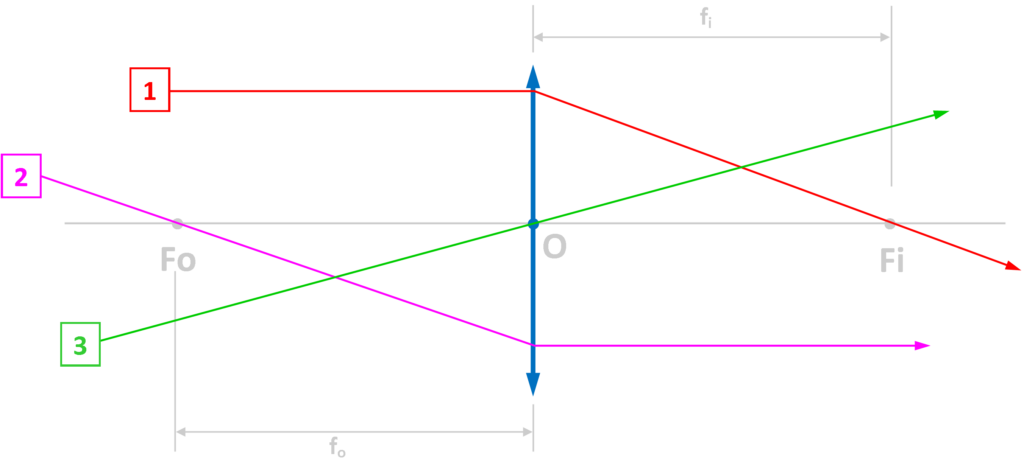
- Tout rayon incident parallèle à l’axe optique est dévié vers le foyer image de la lentille.
- Tout rayon incident passant par le foyer objet de la lentille est dévié et ressort de la lentille parallèlement à l’axe optique
- Tout rayon incident passant par le centre optique de la lentille n’est pas dévié et en, ressort dans son prolongement.
Le plan focal image (PFi) est perpendiculaire à l’axe optique et passe par le foyer image (Fi) sur lequel se forment les images des objets situés à l’infini. Le point Fi2 est un foyer image secondaire de la lentille pour tous les rayons lumineux provenant de la direction I2∞. Si on place un verre dépoli, une pellicule ou un capteur numérique sur ce plan focal, on peut visualiser ou enregistrer les objets vus par la lentille. C’est le principe même de l’appareil photographique. Le plan focal objet (PFo) est le plan perpendiculaire à l’axe optique passant par le foyer objet (Fo) de la lentille. Un objet placé sur le plan foyer objet ne pourra pas être visualisé ; il se forme en effet à l’infini étant donné que les rayons lumineux le composant émergent de la lentille parallèles les uns aux autres.
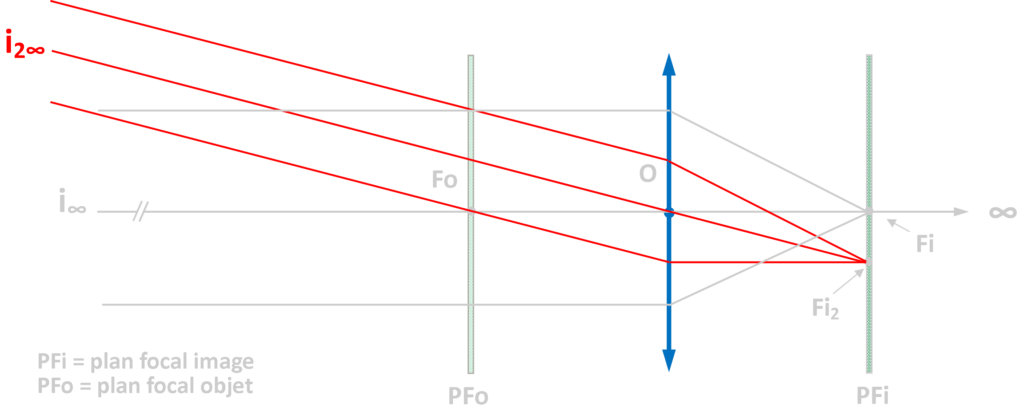
Tout rayon lumineux incident (Ri) est réfracté, passe par le centre optique de la lentille et en ressort parallèlement à lui-même. Si l’on prolonge 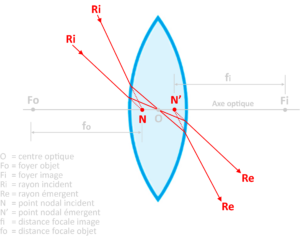 le rayon incident il coupe l’axe optique en un point N. On peut faire de même avec le rayon émergent (Re). On appelle ces points N et N’ les point nodaux de la lentille. Leur emplacement ne varie pas et est fonction de l’épaisseur de la lentille. Plus celle-ci est mince, plus les points nodaux se rapprochent du centre optique. La distance focale se mesure en fait à partir de ces points. Ils revêtent une grande importance dans la construction et les calculs optiques des objectifs. On fera en sorte que le diaphragme soit confondu avec un des points nodaux ou le centre optique de l’objectif, ce qui n’est pas toujours possible techniquement.
le rayon incident il coupe l’axe optique en un point N. On peut faire de même avec le rayon émergent (Re). On appelle ces points N et N’ les point nodaux de la lentille. Leur emplacement ne varie pas et est fonction de l’épaisseur de la lentille. Plus celle-ci est mince, plus les points nodaux se rapprochent du centre optique. La distance focale se mesure en fait à partir de ces points. Ils revêtent une grande importance dans la construction et les calculs optiques des objectifs. On fera en sorte que le diaphragme soit confondu avec un des points nodaux ou le centre optique de l’objectif, ce qui n’est pas toujours possible techniquement.
Image d’un objet situé à l’infini.
En vertu des rayons particuliers et admettant que tous les rayons lumineux proviennent de l’infini, on peut construire le graphique suivant. On s’aperçoit que l’image de cet objet situé à l’infini se construit sur le plan focal image.
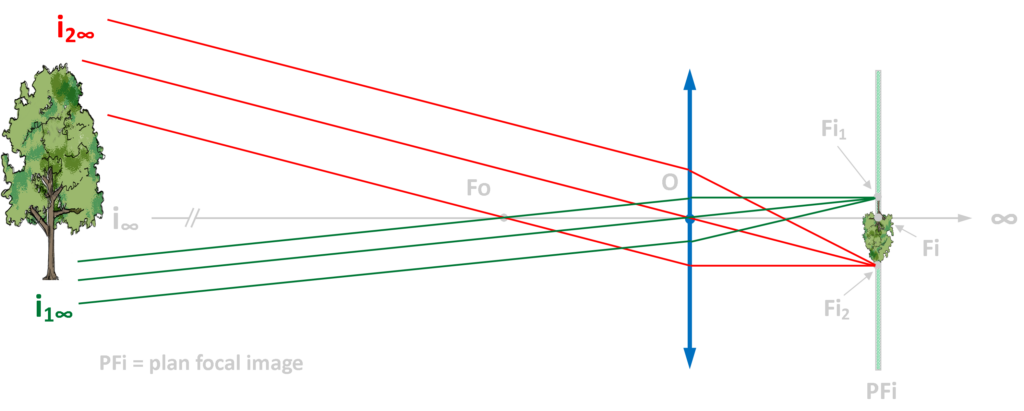
L’infini photographique n’a rien à voir avec l’infini mathématique. En photographie, on considère que tous les objets situé à 1000 fois la focale de l’objectif utilisé sont à l’infini. Ainsi, avec un objectif de 50 mm de focale, tous les sujets situés à 50000 mm (ou 50 m pour être plus clair) se situent à l’infini. Soyons toutefois prudents, cette notion est en effet variable car l’infini photographique aussi appelé hyperfocale (pour une mise au point à l’infini, l’hyperfocale est la distance au-delà de laquelle tous les objets ont une netteté acceptable) varie en fonction de la focale de l’objectif et du diaphragme.
Image d’un objet situé à une distance finie.
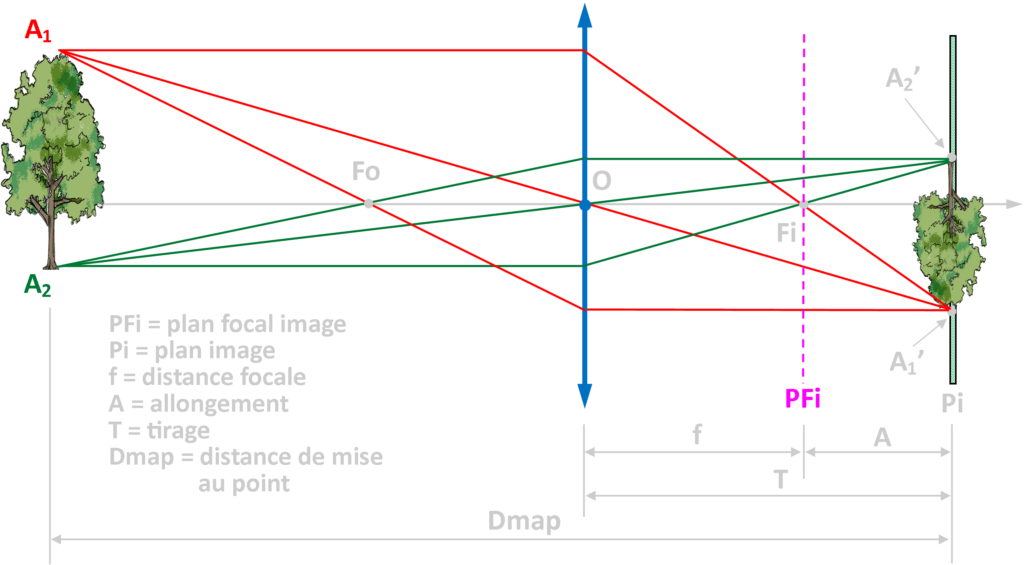
Pour former l’image d’un point situé à une distance inférieure à l’infini, il suffit de former l’image de tous les points qui le composent. A cette fin, isolons un point particulier de cet objet (A1). Ce point émet des rayons dans toutes les directions. Il en est toutefois trois dont nous connaissons le comportement particulier :
- Le rayon parallèle à l’axe optique converge au foyer image.
- Le rayon passant par le foyer objet émerge parallèlement à l’axe optique
- Le rayon passant par le centre optique n’est pas dévié.
Ces trois rayons convergents vers le point A1’ qui est l’image du point A1. On peut procéder de la même façon avec le point A2 qui forme son image au point A2’ ainsi qu’avec tous les points de l’objet. On s’aperçoit que l’image se forme derrière le plan focal image, sur un nouveau plan que l’on appellera le plan image (Pi). A nouveau, si on place un verre dépoli, une pellicule ou un capteur numérique sur ce plan image, on peut visualiser ou enregistrer cette image.
La distance entre le centre optique de l’objectif et le plan image est le tirage (T), celle entre le plan focal image et le plan image est l’allongement (A). La distance de mise au point (Dmap) est toujours la distance comprise entre le sujet et son image (plan focale image ou plan image).
Notions d’objectif.
Eléments et groupes.
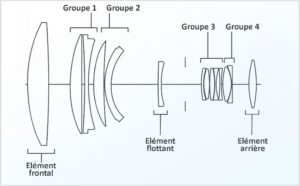 Si on veut obtenir des images de qualité photographique, on ne peut pas se contenter d’une simple lentille convergente. Pour construire un objectif, il faudra donc assembler plusieurs lentilles afin d’assurer la formation d’une image convenable sur le plan du capteur ou de la pellicule. Deux ou plusieurs lentilles assemblées de manière jointives par collage sur la totalité de leur surface ou non constituent un groupe. Une lentille isolée (dont la totalité de la surface est en contact avec l’air) constitue un élément. Les différents groupes et éléments sont séparés par de l’air.
Si on veut obtenir des images de qualité photographique, on ne peut pas se contenter d’une simple lentille convergente. Pour construire un objectif, il faudra donc assembler plusieurs lentilles afin d’assurer la formation d’une image convenable sur le plan du capteur ou de la pellicule. Deux ou plusieurs lentilles assemblées de manière jointives par collage sur la totalité de leur surface ou non constituent un groupe. Une lentille isolée (dont la totalité de la surface est en contact avec l’air) constitue un élément. Les différents groupes et éléments sont séparés par de l’air.
Les axes de toutes les lentilles doivent être alignés sur l’axe optique de l’objectif pour obtenir un système centré (contrairement aux objectifs à décentrement et bascules par exemple). Le plan principal de l’objectif est perpendiculaire à son axe optique. C’est dans ce plan que les constructeurs s’efforceront de placer le diaphragme. On comprend facilement que dans de tels systèmes optiques plus ou moins complexes, les rayons lumineux sont réfractés de diverses façons par les différentes lentilles constituant les groupes et les éléments ; ils ne suivent donc pas un trajet rectiligne.
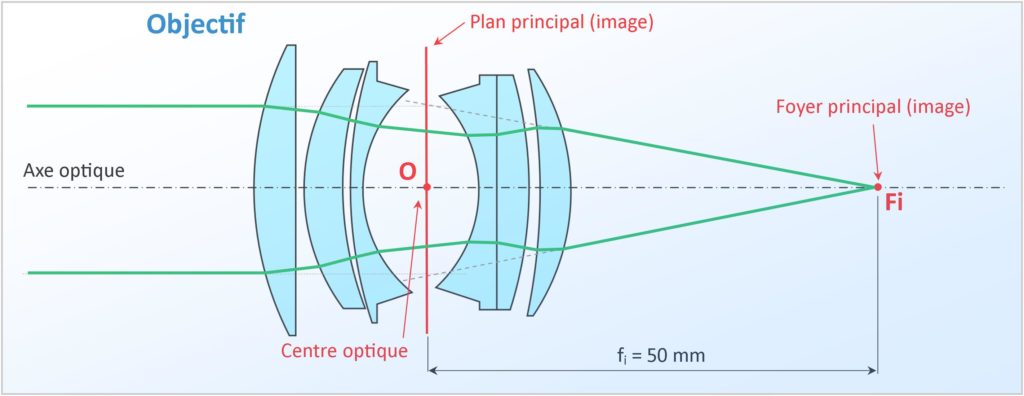
Toutefois, pour la simplicité du raisonnement, nous continuerons à assimiler un objectif (quel que soit le nombre de lentilles qui le constituent) à une lentille convergente mince de distance focale équivalente.
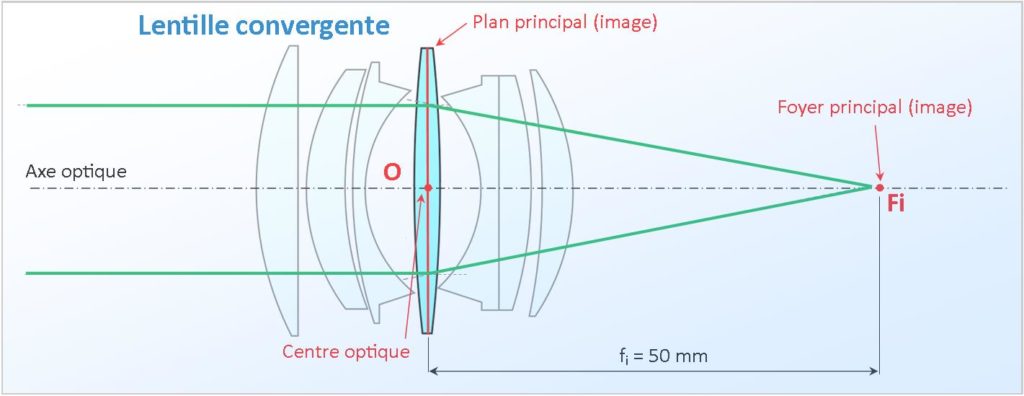
La mise au point dans les objectifs photographiques.
Nous avons vu plus haut que si la mise au point d’un objectif est effectuée sur l’infini, une image nette de l’objet se forme sur le plan focal image (situé au foyer image de l’objectif et où se trouve le capteur photographique) ; le plan image est donc confondu avec le plan focal image. Par contre, si le sujet se trouve à une distance finie de l’appareil photographique et si l’objectif est toujours réglé sur l’infini, cette image se formera en arrière du plan focal image (le plan image n’est plus confondu avec le plan focal image) et l’image formée sur le capteur n’est pas nette. Afin d’effectuer la mise au point, il suffira de déplacer le centre optique de l’objectif vers l’avant d’une distance égale à celle séparant le plan image du plan focal image : l’allongement. Ceci revient à augmenter le tirage de l’objectif.
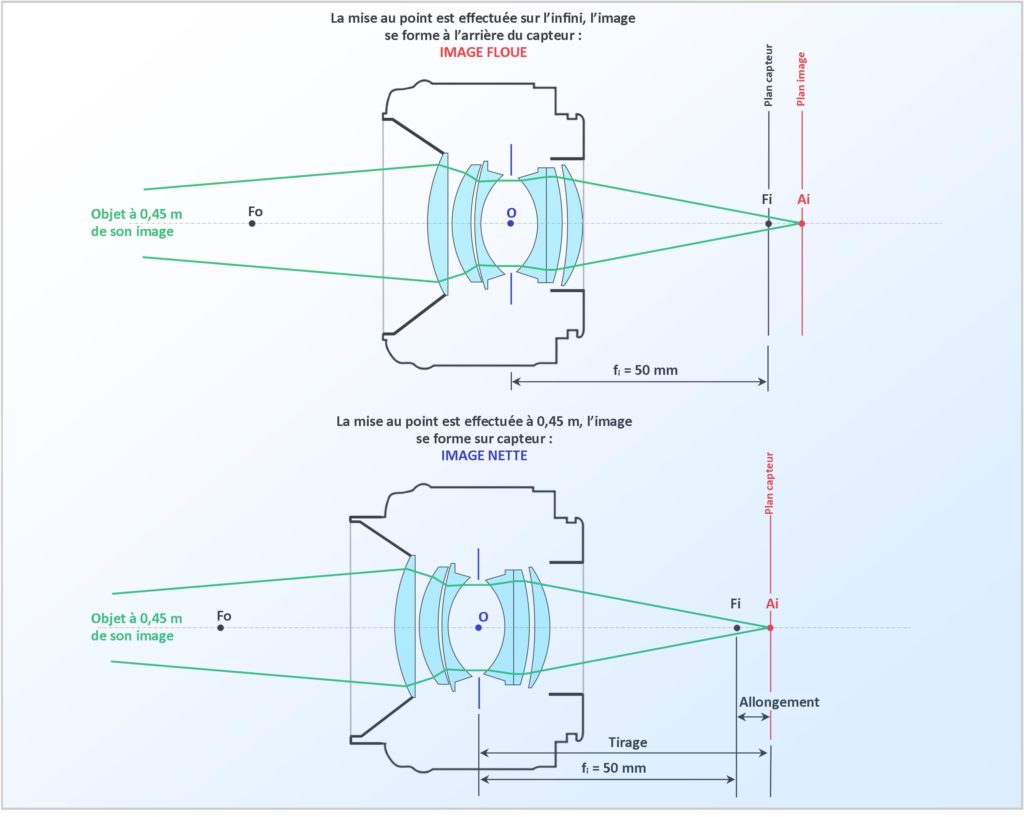
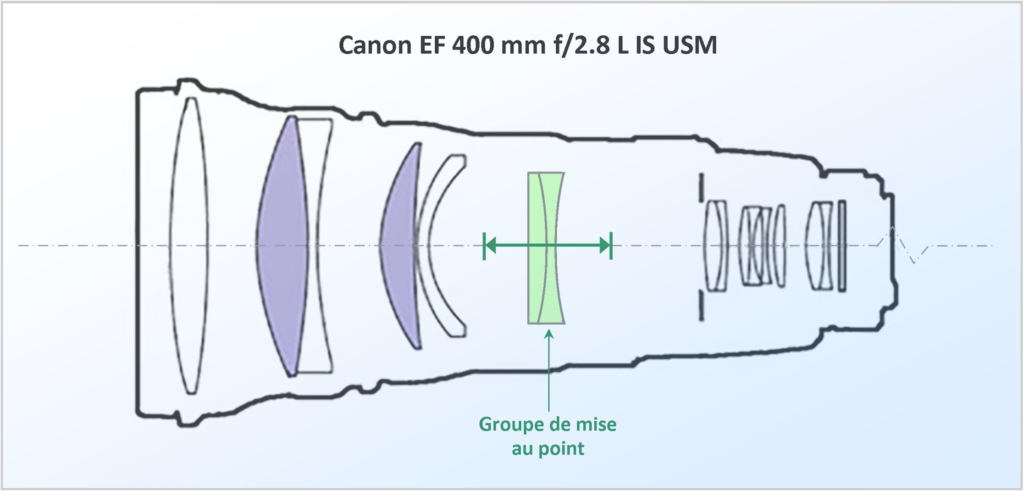
Dans un appareil photographique, la mise au point se fait par déplacement de l’ensemble des lentilles (groupes et éléments) constituant l’objectif ou d’une partie seulement d’entre eux (groupes ou éléments flottant de mise au point). Elle est optimale quand la surface photosensible (pellicule ou capteur) coïncide avec le plan où se forme l’image de l’objet à photographier.
Angle de champ et cercle image
Tout objectif a un « champ de vision » limité à un certain angle. Les objets situés hors de cet angle de champ ne sont pas « vus » par l’objectif et de ce fait ne figurent pas sur l’image. L’objectif ayant une section circulaire, l’image qu’il forme est évidement ronde : c’est le cercle image brut caractérisé par son diamètre. On sait que la qualité de l’image diminue en périphérie de ce cercle image en raison des aberrations et déformations qui apparaissent au pourtour de l’image. Il existe donc, à l’intérieur de ce cercle image brut un autre dans lequel l’ensemble de l’image est net et dépourvu de toute chute de lumière, aberration, déformation ou perte de qualité ; le cercle d’image utile. L’ensemble du rectangle formé par le capteur doit impérativement s’inscrire à l’intérieur de ce cercle image utile dont le diamètre doit être au moins égal à la diagonale du format à couvrir. Dans le cas contraire, les coins de l’image vont s’assombrir. On dit que l’objectif ne couvre pas le format et qu’il y a vignettage.
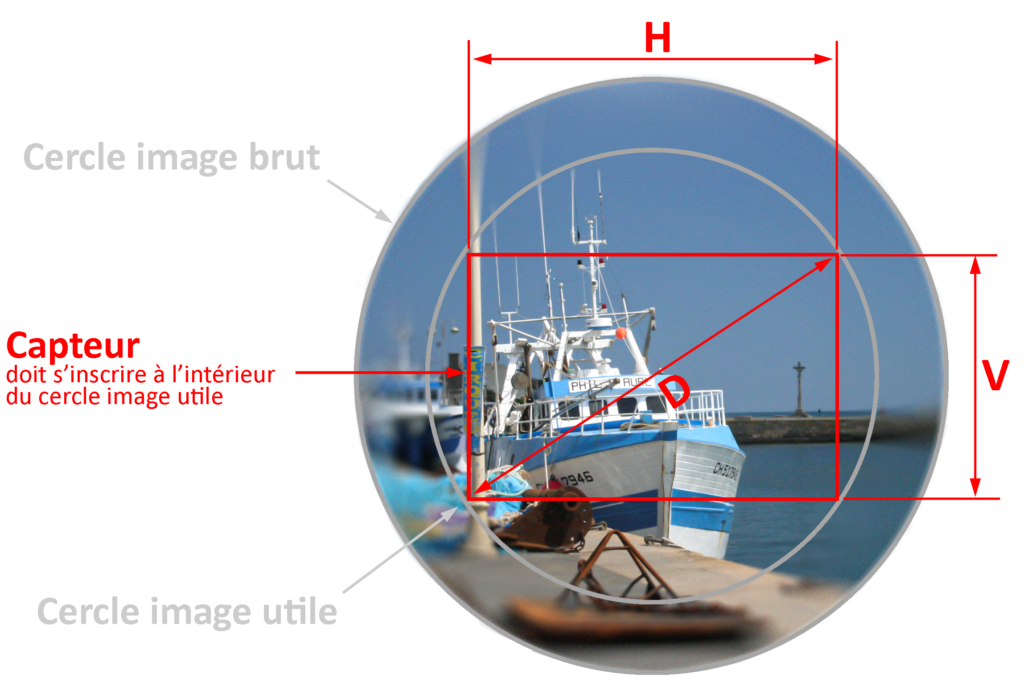
Il est facile de calculer cette diagonale à l’aide de la formule de Pythagore D = √ (V2 + H2)
on trouve ainsi : 43 mm pour le plain format 24×36
28,6 mm pour le format APS-C
27 mm pour le format APS-C Canon
Pratiquement, les objectifs ont un cercle image brut dont le diamètre est légèrement supérieur à la diagonale du format à couvrir.
 Quoiqu’empirique et subjective, il existe une méthode pour mesurer l’angle de champ d’un objectif. Installons celui-ci au-dessus d’une feuille de papier à une distance plus ou moins égale à sa focale. Au préalable, nous aurons fermé son diaphragme à 16 et effectué la mise au point à l’infini. Eclairons-le à l’aide d’un luminaire par exemple et affinons la distance par rapport à la feuille de papier jusqu’à ce que l’image du luminaire soit nette. Maintenant la feuille de papier se situe sur le plan focal image de l’objectif. Il nous suffit maintenant de mesurer l’image formée.
Quoiqu’empirique et subjective, il existe une méthode pour mesurer l’angle de champ d’un objectif. Installons celui-ci au-dessus d’une feuille de papier à une distance plus ou moins égale à sa focale. Au préalable, nous aurons fermé son diaphragme à 16 et effectué la mise au point à l’infini. Eclairons-le à l’aide d’un luminaire par exemple et affinons la distance par rapport à la feuille de papier jusqu’à ce que l’image du luminaire soit nette. Maintenant la feuille de papier se situe sur le plan focal image de l’objectif. Il nous suffit maintenant de mesurer l’image formée.
 J’ai effectué les mesures pour deux objectifs : Canon EF 50mm f/1.4 (conçu pour le plein format) et Canon EF-S 18-135mm f/3.5-5.6 (conçu pour le format APS-C Canon). La figure ci-dessus montre que le diamètre du cercle image brut de l’objectif plein format est de 56 mm tandis que celui du cercle image utile est de 44 mm. Pour l’objectif APS-C, j’ai mesuré 36 et 28 mm respectivement.
J’ai effectué les mesures pour deux objectifs : Canon EF 50mm f/1.4 (conçu pour le plein format) et Canon EF-S 18-135mm f/3.5-5.6 (conçu pour le format APS-C Canon). La figure ci-dessus montre que le diamètre du cercle image brut de l’objectif plein format est de 56 mm tandis que celui du cercle image utile est de 44 mm. Pour l’objectif APS-C, j’ai mesuré 36 et 28 mm respectivement.
Calculons maintenant l’angle de champ de cet objectif.
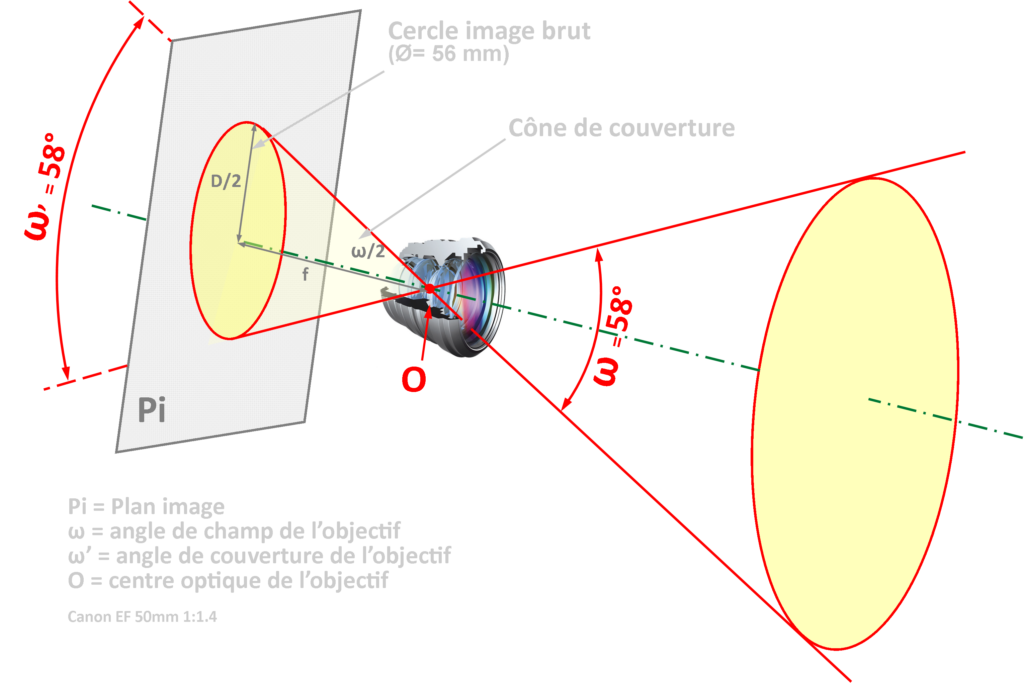

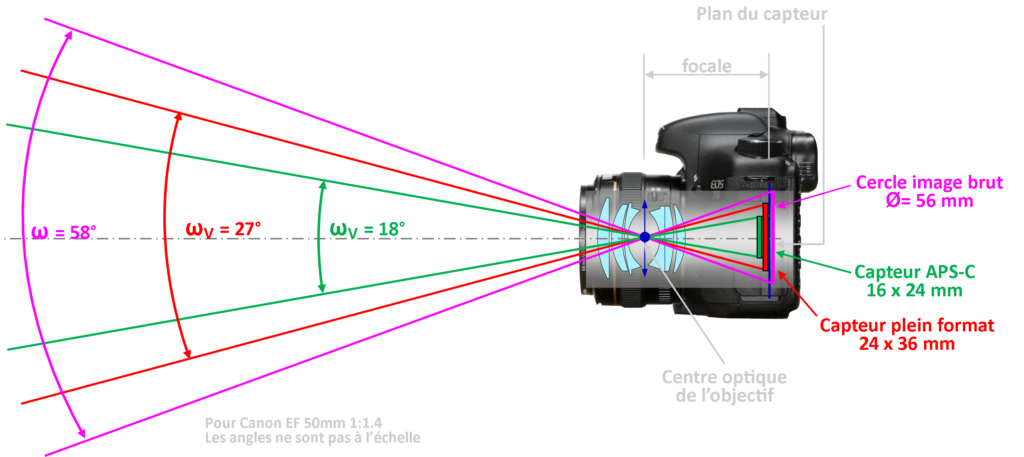
Pour l’objectif plein format on trouve donc un angle de champ de 58 degrés correspondant au cercle d’image brut. Un angle de champ de 47 degrés correspondra quant à lui au cercle d’image utile. On voit que l’angle de champ varie en fonction de la focale de l’objectif et du diamètre du cercle image qui correspond au format que l’on utilise. On comprend aussi que la construction et la formule optique des objectifs dits plein format et APS-C n’est pas identique. En effet le cercle image d’un objectif APS-C ne doit pas nécessairement être aussi grand que celui d’un plein format.

C’est la raison pour laquelle la plupart des constructeurs produisent deux types d’objectifs adaptés aux deux grands types de capteurs, 24×36 ou APS-C. Quand il s’agira de faire un choix, n’oublions pas qu’un objectif conçu pour le plein format sera utilisable aussi bien avec un capteur plein format que APS-C. l’inverse n’est pas vrai. En effet, un capteur 24×36 sera plus grand que le champ couvert par un objectif APS-C et il y aura vignettage (comme on peut le voir sur la figure ci-dessus). Chez Canon, un objectif EF est utilisable sur un boîtier plein format (EOS 1D, 6D et 5D) ainsi que sur un boîtier APS-C. Par contre, il sera mécaniquement impossible de monter un objectif EF-S sur un boîtier plein format et il ne pourra dès lors être utilisé que sut un boîtier APS-C. Chez Nikon les deux types d’objectif peuvent être montés sur les deux types de boîtiers ; les appareils photo au format FX corrigent le fait que l’image circulaire DX est plus petite que le capteur plein format en activant uniquement les pixels correspondant à la taille d’un capteur DX.
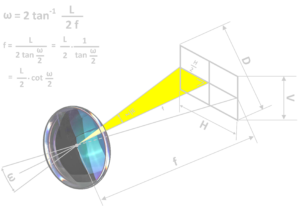 On peut calculer les angles de champ verticaux, horizontaux et diagonaux en fonction de la taille du capteur et de la focale de l’objectif.
On peut calculer les angles de champ verticaux, horizontaux et diagonaux en fonction de la taille du capteur et de la focale de l’objectif.
La démonstration de cette formule a déjà été faite plus haut, je n’y reviendrai donc plus.
Ici, L figure la largeur du format utilisé (H pour « horizontal »), sa hauteur (V pour « vertical ») ou sa diagonal (D).
- ω = angle de vision
- L = dimension du capteur
- f = focale
L’angle de champ (ici l’angle de champ vertical ωV) varie avec la taille du capteur
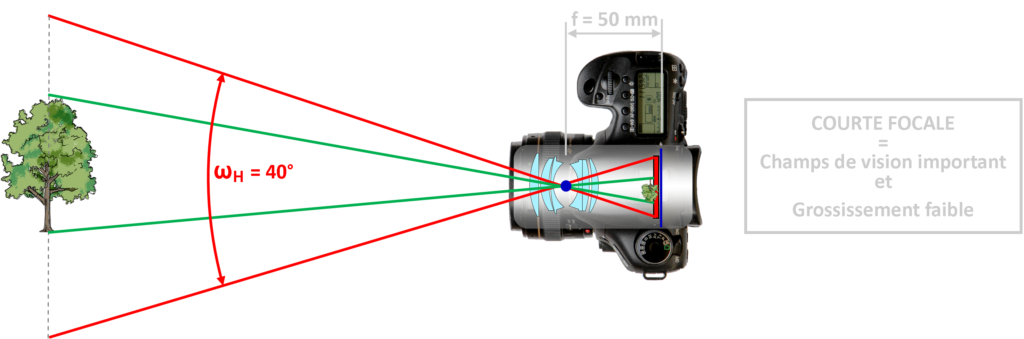
L’angle de champ (ici l’angle de champ horizontal ωH) varie avec la focale
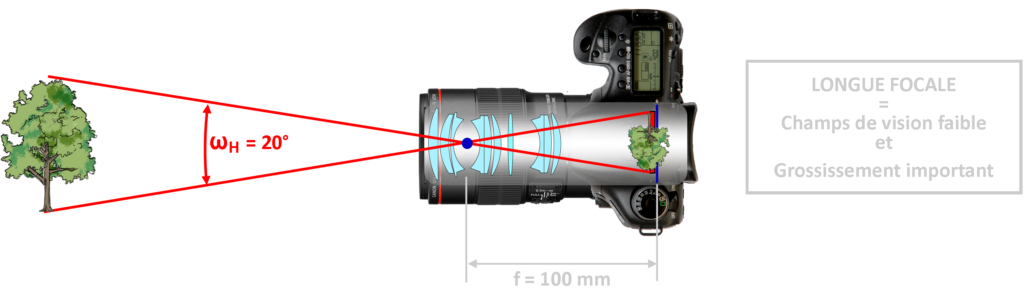
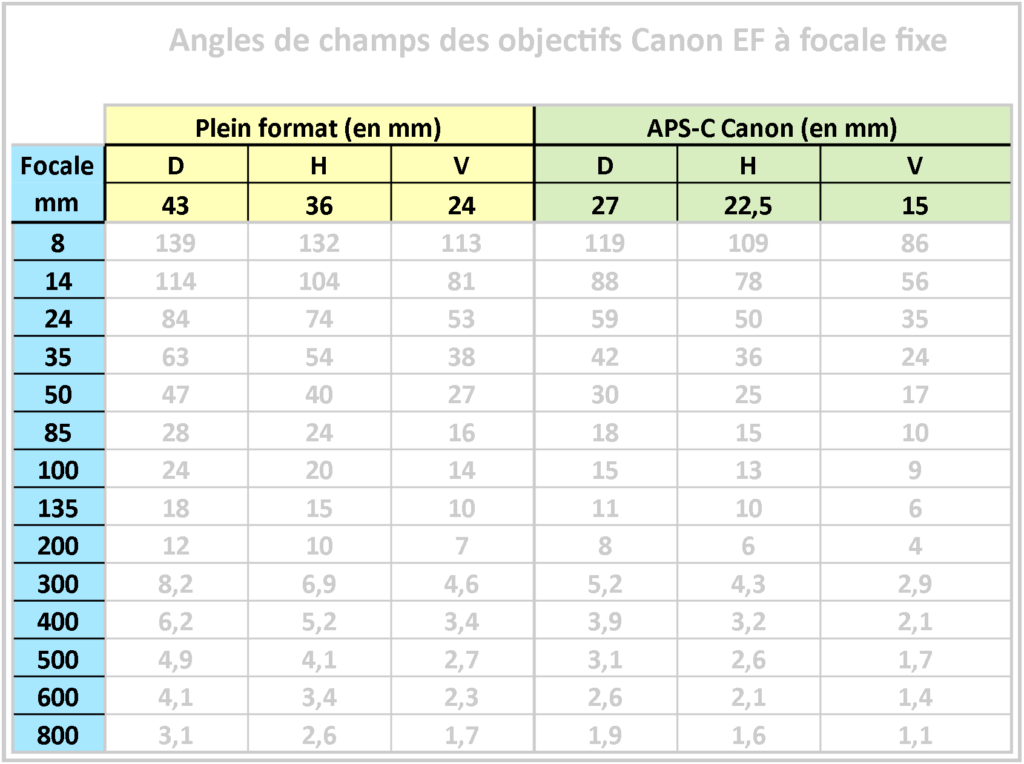
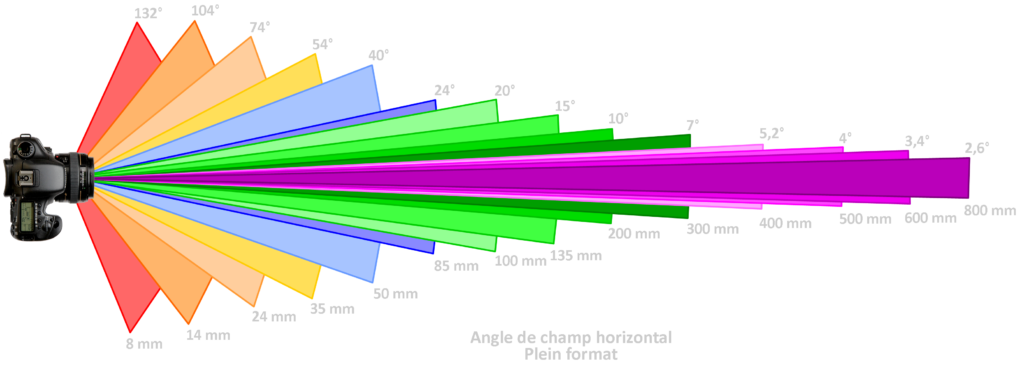
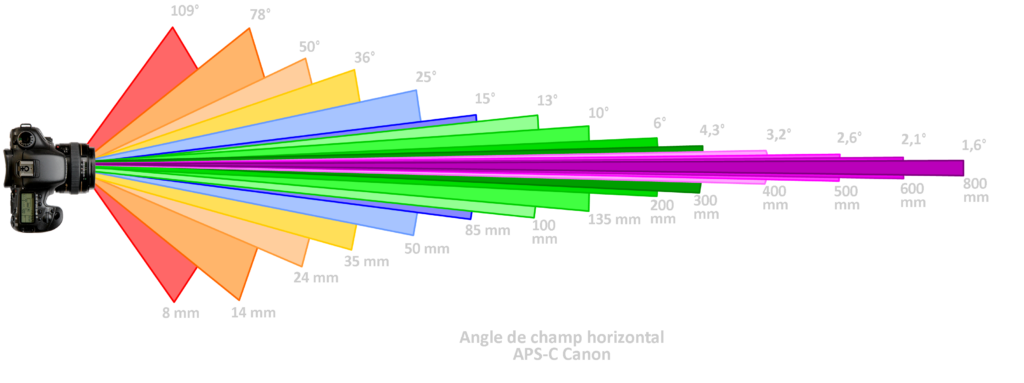
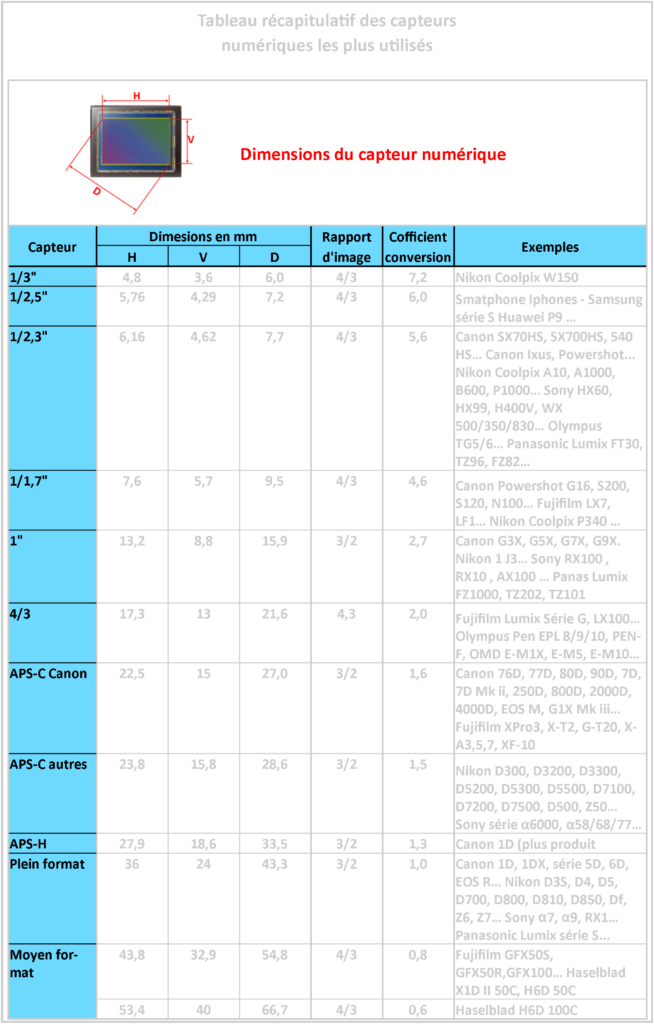
Vous trouverez ci-après un récapitulatif des angles de champs de champ diagonaux, horizontaux et verticaux pour les capteurs plein format (FF), APS-c Canon et 1/1,3’’ (Nikon Coolpix A1000).

Focale équivalente ou corrigée.
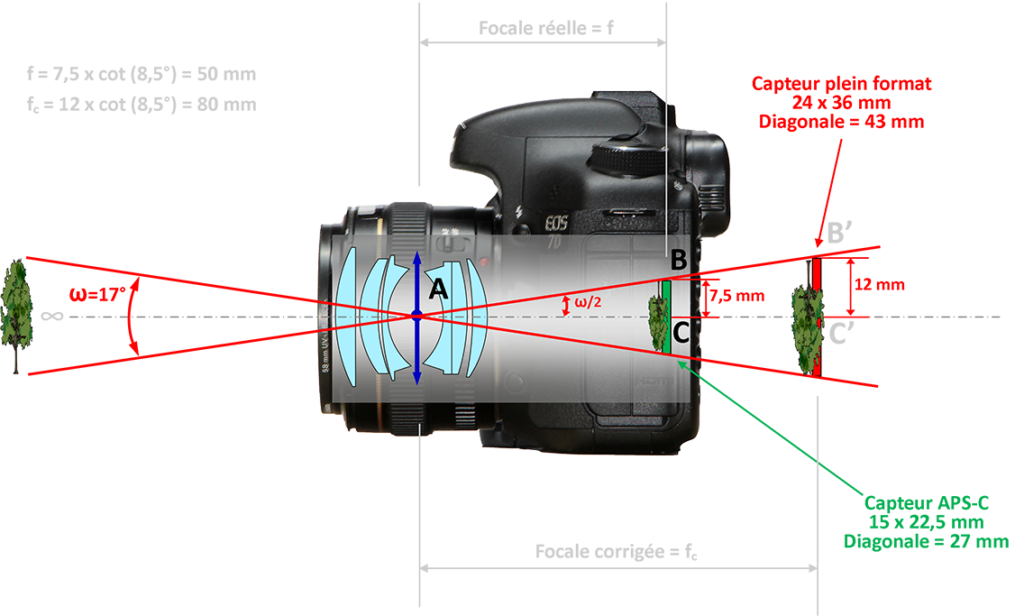
Comme nous l’avons dit au début de cet article, en photographie, la distance focale équivalente en 35 mm ou 24×36 est une mesure qui indique l’angle de vue particulier à un objectif d’appareil photo combiné à un type de pellicule ou de capteur de taille déterminée qui produirait le même cadrage sur un capteur 24×36. La distance focale équivalente en 35 mm d’un couple objectif-capteur donné est la distance focale qui serait nécessaire sur un appareil photo argentique 35 mm pour obtenir le même angle de vue. Autrement dit, en partant d’une combinaison objectif/boîtier APS-C (par exemple), quelle devrait être la focale d’un objectif que je monterais sur un boîtier équipé d’un capteur plein format pour qu’il ait le même angle de champ ? Dans la figure suivante, je considère le cas d’un boîtier APS-C équipé d’un objectif de 50 mm de focale. Je peux donc en vertu de la formule de l’angle de champ en fonction de la focale et de la taille du capteur calculer l’angle de champ vertical (cadrage paysage) de l’ensemble à 17 degrés.
Dans les triangles rectangle ABC et AB’C’, respectivement AC=BC cot αA et AC’=B’C’ cot αA. Donc :
- AC = 7.5 mm x cot(8.5°) = 50 mm = focale de l’ensemble objectif/capteur
- AC’ = 12 mm x cot(8.5°) = 80 mm = focale équivalente 24×36
Si nous partons de la dernière formule de l’encadré ci-dessus, nous pouvons faire le raisonnement suivant :

Le même développement peut être fait avec les autres dimensions du capteur (H ou D). Ceci nous donne un facteur de correction uniquement en fonction de la taille du capteur. Ainsi :
- Le facteur de correction pour APS-C Canon est de 24/15 ou 36/22,5 ou 43/27 = 1,6
- Le facteur de correction pour APS-C Nikon est de 24/15,8 ou 36/23,8 ou 43/28,6 = 1,5
- La focale corrigée de l’exemple de la figure est de 50 x 1.6 = 80 mm.
Il est maintenant possible d’attribuer un facteur de correction à chaque type de capteur en fonction de ses dimensions physiques.
Conclusion.
Considérons les points de comparaisons suivants :
Grandissement.
Bien que rarement utilisé en photographie normale, le grandissement est le rapport de la dimension de l’image enregistrée sur le capteur de l’appareil photo sur la dimension réelle du sujet photographié. Le grandissement G = taille de l’image sur le capteur/ taille réelle de l’objet. Par exemple :
1. Si vous photographiez un objet de 2 cm et que l’image de ce même objet mesure 1 cm sur le capteur, alors on a un rapport de grandissement de 1/2 (souvent noté 1:2), ou un facteur de grandissement de 0,5x.
2. Si l’image de ce même objet mesure 2 cm sur le capteur, le rapport de grandissement sera de 1/1 (1:1), le facteur de 1x
Perspective
La perspective, telle que je l’entends ici, fait référence à la dimension des objets ainsi que la distance entre eux.
Le grand angle permet d’inclure plus d’éléments dans votre photo pour aider à la mise en contexte. Par contre, il tend à étirer la perspective, c’est-à-dire donner l’impression que les différents plans dans l’image son plus loin les uns des autres. Au contraire, le téléobjectif vous permet de vous rapprocher virtuellement de votre sujet et donner l’impression que les différents plans sont plus près les uns des autres.
Les photos suivantes sont composées de quatre plans distincts. En s’éloignant du point de prise de vue : le salon de jardin et le parasol, le rosier blanc, le saule et enfin l’abri de jardin. On s’aperçoit que, en augmentant la focale, ces différents plans semblent de plus en plus proches les uns des autres. La perspective est donc modifiée par le changement de focale, l’image « s’écrase » en augmentant la focale.

Grossissement
La notion de grossissement employée pour l’observation au moyen d’un instrument (une lunette d’observation ou des jumelles par exemple) peut être considérée de différentes façons :
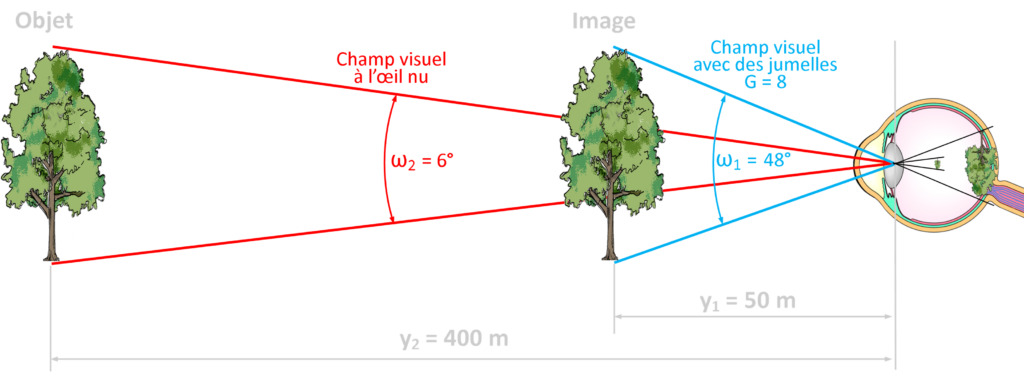
- A l’œil nu, l’image qui se forme sur notre rétine a une certaine taille. L’observation du même objet au moyen d’un instrument d’observation produit une image sur la rétine d’une taille différente, habituellement plus grande. Le rapport entre ces deux dimensions de l’image est le grossissement. Cette notion est théorique puisqu’il est impossible de mesurer directement l’image au niveau de la rétine.
- Avec un instrument d’observation, on voit l’objet comme s’il était situé à une autre distance de l’observateur, distance généralement plus petite. Le grossissement est le rapporte entre ces deux distances. Ainsi, des jumelles grossissant 8 fois me donneront l’impression que le sujet est 8 fois plus proche de moi. Cette notion de rapprochement est celle qui est le plus souvent associée au grossissement par le plus grand nombre d’entre nous.
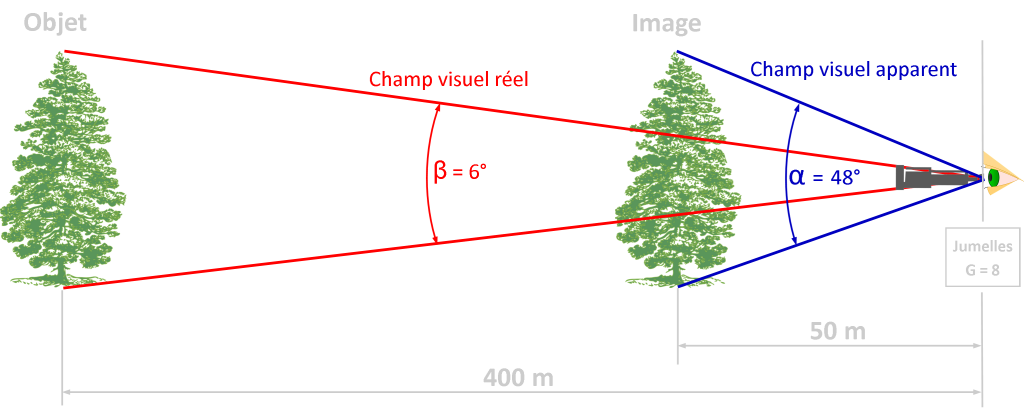
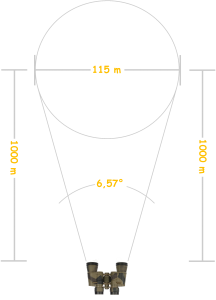
- En fait, tout ceci n’est qu’une question d’angles. La dimension angulaire d’un objet est l’angle formé par les points extrêmes de l’objet et l’œil de l’observateur. Au travers d’un instrument optique, cet angle est différent, généralement plus grand et le rapport entre ces deux dimensions angulaires représente le grossissement. G = ω1/ω2 = 48/6 = 8
Pouvons-nous dresser un parallèle entre grossissement et focale d’un objectif ?
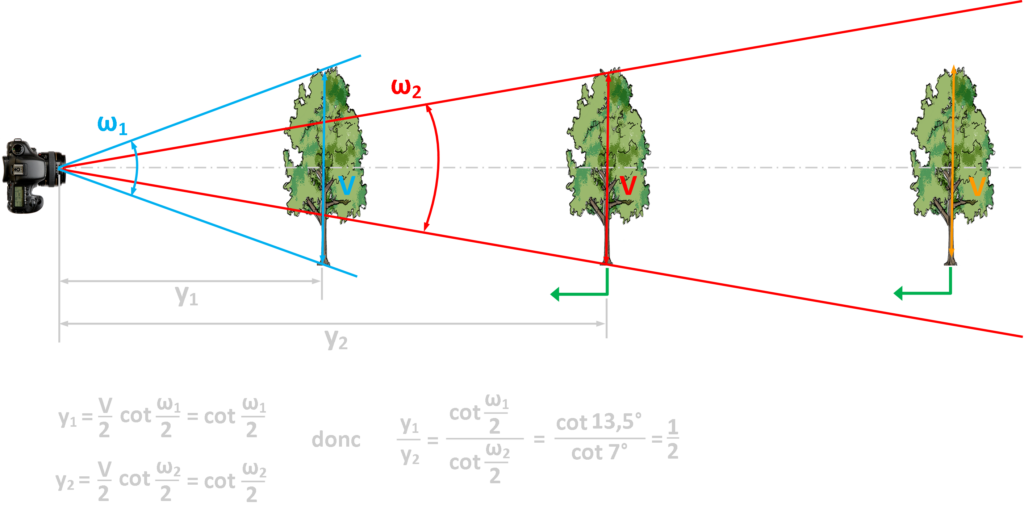
Acceptons tout d’abord la notion suivante (que je ne vais pas développer ici mais qui est admise par bon nombre de photographes) : une focale de 50 mm sur un capteur plein format correspond plus ou moins à la vision humaine, et produit un grossissement de 1X.
Imaginons un reflex plein format que nous équipons d’abord d’un objectif de 50 mm de focale dont l’angle de champ vertical est de 27°. Afin qu’un objet de taille V occupe toute la hauteur du capteur, nous devons nous trouver à une distance de l’objet égale à Y1. Changeons maintenant l’objectif pour un 100 mm dont l’angle de champ vertical est de 14°. Si nous voulons une fois de plus que ce même objet de taille V occupe toute la hauteur de notre capteur, nous devons nous déplacer à une distance Y2 égale à deux fois Y1. Dès lors, avec un 100 mm, un objet semble deux fois plus proche qu’il n’est en réalité (« grossissement » de 2X). Augmentons la focale à 200 mm et nous voyons qu’Y2 est maintenant égale à quatre fois Y1 (« grossissement » de 4X).
De plus, le tableau des angles de champs plus haut montre un rapport de 1/2 à chaque doublement de focale impliquant un doublement du « grossissement ».
Par exemple : 50 mm = 27° et G = 27/27 ≈ 1
100 mm = 14° et G = 27/14 ≈ 2
200 mm = 7° et G = 27/7 ≈ 4
400 mm = 3,4° et G = 27/3,4 ≈ 8
800 mm = 1,7° et G = 27/1,7 ≈ 16
Donc on peut considérer que le « grossissement » produit par un objectif vaut sa longueur focale divisée par 50.
Comparons deux images brutes.
Observons les deux images suivantes. Celle de gauche a été réalisée au moyen d’un appareil équipé d’un capteur plein format muni d’un objectif de 50 mm de focale ; celle de droite avec le même objectif mais cette fois avec un boîtier contenant un capteur APS-C. La taille de ces deux photos est proportionnelle à celle des capteurs respectifs

1. La taille du segment de 60 cm sur la barre à l’avant plan a la même taille sur les deux images (en fait capteurs) : le grandissement ne change pas.
2. La perspective sur les deux photos reste la même : la perspective n’est pas affectée.
3. La taille des objets sur les deux photos ainsi que l’angle sous lequel ils sont représentés ne varient pas : le « grossissement » ne change pas.
Seul le cadrage de la prise de vue change. Les deux capteurs « voient » exactement la même scène. L’image en plein format est tout simplement rognée de façon à se limiter à ce que couvre le capteur APS-C.

Comparons deux tirages de même taille.
Observons les deux images suivantes. Celle du haut a été réalisée au moyen d’un appareil équipé d’un capteur plein format muni d’un objectif de 50 mm de focale ; celle du bas avec le même objectif mais cette fois avec un boîtier contenant un capteur APS-C. Nous avons réalisé un tirage de ces deux photos à une taille de 30 X 20 cm.

1. La taille du segment de 60 cm sur la barre à l’avant plan n’a plus la même taille sur les deux images (ou tirages) : le rapport de reproduction (ou rapport d’impression) varie et passe de 1/12 sur le tirage du haut à 1/7 sur celui du bas.
2. La perspective sur les deux tirages change : la perspective sur la photo du bas semble plus « écrasée ».
3. Les objets sur les deux photos ainsi que l’angle sous lequel ils sont représentés sont cette fois différents. La taille du segment de 60 cm sur la barre à l’avant plan n’a plus la même taille sur les deux images (ou tirages), 5,2 cm contre 8,6 cm. Si, encore, nous acceptons qu’une focale de 50 mm sur un plein format produit un « grossissement » de 1X, il vaut sur le tirage du bas 8,6 / 5,2 = 1.6X. Nous pouvons encore dire que la focale équivalente sur le tirage du bas est de 50 x 1,6 = 80 mm.
Ces mêmes différences seront visibles aussi à travers le viseur ou sur l’écran de l’appareil en mode de prise de vue « Life View ».
Etant donné que la taille du capteur n’a d’incidence que sur le rendu de la focale de l’objectif et ce uniquement sur un tirage de même format, je préfère remplacer les termes de « focale équivalente » ou « coefficient multiplicateur » par « facteur de recadrage » ou « crop factor ».
La mention de « focale équivalente » conduit à diverses fausses croyances, voire affirmations. Il y en a deux que l’on entend régulièrement :
- « Un capteur APS-C me permet d’avoir une image plus proche de mon sujet ». Evidement le sujet sera plus grand sur le tirage, mais ceci est dû uniquement à un recadrage et non à une augmentation optique. Imaginez découper une partie d’une photo et ensuite l’agrandir à la photocopieuse.
- « Avec un capteur APS-C, je bénéficie d’une plus longue focale donc la profondeur de champ sera plus réduite et le sujet sera plus isolé de l’arrière-plan ». Vu que la profondeur de champ (Pdc) n’est fonction que de la distance de mise au point (Dmap) qui ne change pas avec un capteur de petite taille, et de l’hyperfocale.
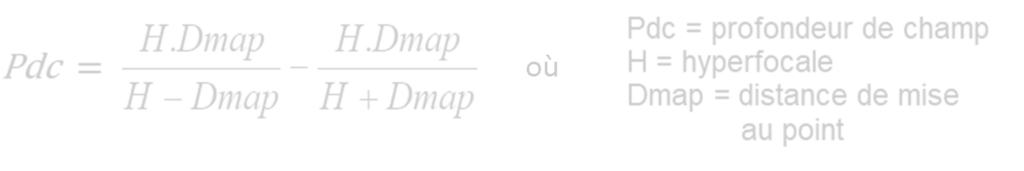
Cette même hyperfocale est fonction de la focale réelle de l’objectif et le l’ouverture de celui-ci, qui ne varient pas non plus.

On voit donc que le facteur de recadrage ne modifie en aucun cas la profondeur de champ.
Télécharger le PDF en français



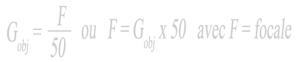
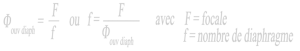
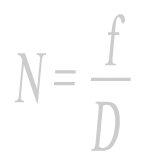

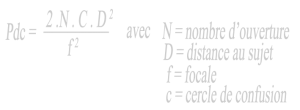





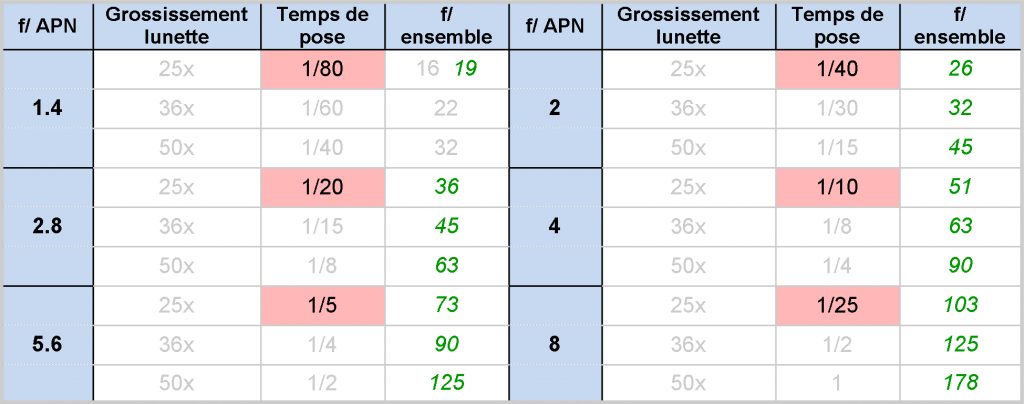
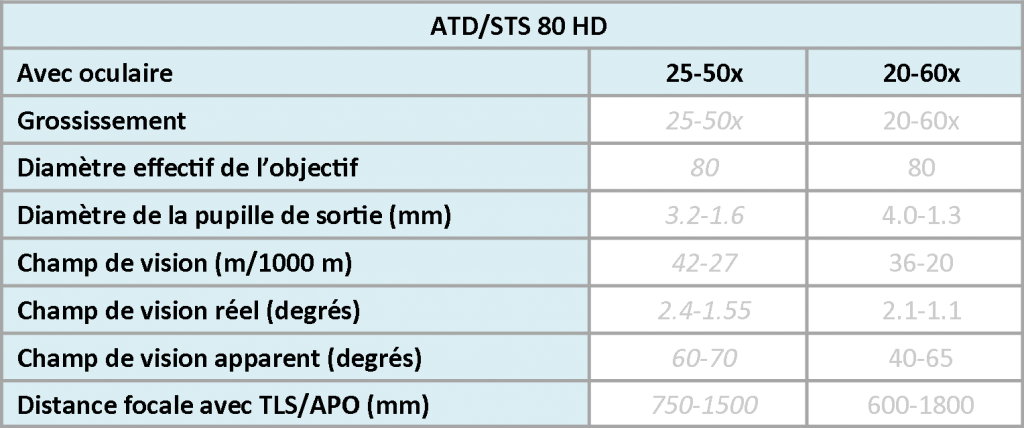
 Régler la focale à l’équivalent de 50 mm en plein format présente plusieurs avantages. On conserve le grossissement de la lunette et on évite le vignettage. A une focale moins élevée, le grossissement de la lunette sera diminué d’un facteur valant sa valeur divisée par 50 (36x deviendra à 24 mm de focale 36x(24/50)=17.2 par exemple). Aussi, le champ de vision de l’objectif est tellement large que l’on constate un vignettage important que l’on ne peut supprimer même en fermant le diaphragme au maximum. À une focale plus élevée, l’ouverture utile diminuera de telle sorte que le temps de pose augmentera de manière significative (flou de mouvement de votre sujet) ou il faudra monter en ISO (augmentation du bruit encore acceptable jusqu’à 400 ISO et difficile à traiter au-delà)
Régler la focale à l’équivalent de 50 mm en plein format présente plusieurs avantages. On conserve le grossissement de la lunette et on évite le vignettage. A une focale moins élevée, le grossissement de la lunette sera diminué d’un facteur valant sa valeur divisée par 50 (36x deviendra à 24 mm de focale 36x(24/50)=17.2 par exemple). Aussi, le champ de vision de l’objectif est tellement large que l’on constate un vignettage important que l’on ne peut supprimer même en fermant le diaphragme au maximum. À une focale plus élevée, l’ouverture utile diminuera de telle sorte que le temps de pose augmentera de manière significative (flou de mouvement de votre sujet) ou il faudra monter en ISO (augmentation du bruit encore acceptable jusqu’à 400 ISO et difficile à traiter au-delà)

 le flou de bougé qu’en montant en ISO avec une nouvelle fois une augmentation de bruit difficile voire impossible à gérer. N’oublions enfin pas qu’il est conseillé de viser un temps de pose au moins égal à l’inverse de la focale afin d’éviter, précisément, tout flou de bouger (à 25x, le temps de pose devrait être de 1/1250 de seconde et à 36x de 1/1800 !!!). Cela restera très difficile à obtenir, ayons donc pour but un temps de pose le plus court possible.
le flou de bougé qu’en montant en ISO avec une nouvelle fois une augmentation de bruit difficile voire impossible à gérer. N’oublions enfin pas qu’il est conseillé de viser un temps de pose au moins égal à l’inverse de la focale afin d’éviter, précisément, tout flou de bouger (à 25x, le temps de pose devrait être de 1/1250 de seconde et à 36x de 1/1800 !!!). Cela restera très difficile à obtenir, ayons donc pour but un temps de pose le plus court possible.